Moderacja i mediacja

Wpływ “trzeciej” zmiennej na relację między dwoma zmiennymi. Moderacja i mediacja to forma analizy regresji, która pozwala badaczom analizować, w jaki sposób trzecia zmienna wpływa na związek zmiennej predykcyjnej i wynikowej.

Jest to ten szczególny przypadek, gdy słowa rozumiane potocznie mają inne znaczenie niż przyjęto rozumieć je w statystyce. Wyjaśniam więc różnicę między moderatorem a mediatorem.

Moderator to zmienna, której wartość decyduje o kierunku lub sile zasadniczej zależności. Obecność istotnego moderatora można sprawdzić wykorzystując analizę wariancji MANOVA¹.

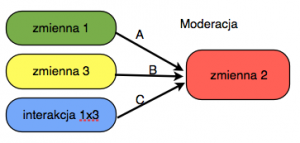
Zasadniczą zależność obrazuje na rysunku strzałka A - istotność związku zmiennych 1 i 2 jest świadectwem istnienia podstawowej zależności. Świadectwem, że jakaś trzecia zmienna stanowi moderator tej zależności jest natomiast istotność strzałki C; nie ma przy tym znaczenia, czy zależność obrazowana strzałką B jest istotna, czy nie. W klasycznych kategoriach analizy wariancji dowodem na to, że zmienna 3 ma status moderatora związku zmiennych 1 i 2 jest istotna interakcja zmiennych 1 i 3 w wyznaczaniu natężenia 1-2 (ta ostatnia ma więc status zmiennej zależnej, podczas gdy 1 i 3 są w schemacie eksperymentu zmiennymi niezależnymi).

Typowa sytuacja, w której poszukuje się moderatorów, to występowanie zależności słabej, która czasami występuje, a czasami zanika, jak np. wpływ postaw na zachowanie. Identyfikacja moderatorów ma więc duże znaczenie praktyczne, pozwala bowiem określić warunki, w których jakaś zależność występuje i odróżnić je od warunków, w których zależność zanika, nawet jeżeli nie rozumiemy dlaczego tak się dzieje.

Główna różnica między prostą interakcją, taką jak w modelach ANOVA lub modelach moderacji, polega na tym, że mediacja zakłada istnienie sekwencji przyczynowej. W tym przypadku wiemy, że stres powoduje zły wpływ na zdrowie, więc byłby to czynnik przyczynowy. Niektóre zmienne predykcyjne wchodzą w interakcje w pewnej (wiadomej z teorii lub badań) kolejności, a nie wpływają na zmienną wynikową pojedynczo lub jako grupa (jak w regresji).

Mediatorami są natomiast z reguły stany lub procesy psychiczne pośredniczące między jakąś zmienną niezależną a jakąś zmienną zależną (można o nich myśleć jak o zasobach lub deficytach). Sposób ich identyfikacji przedstawia poniższy rysunek (trójkątny diagram w lewym górnym rogu).

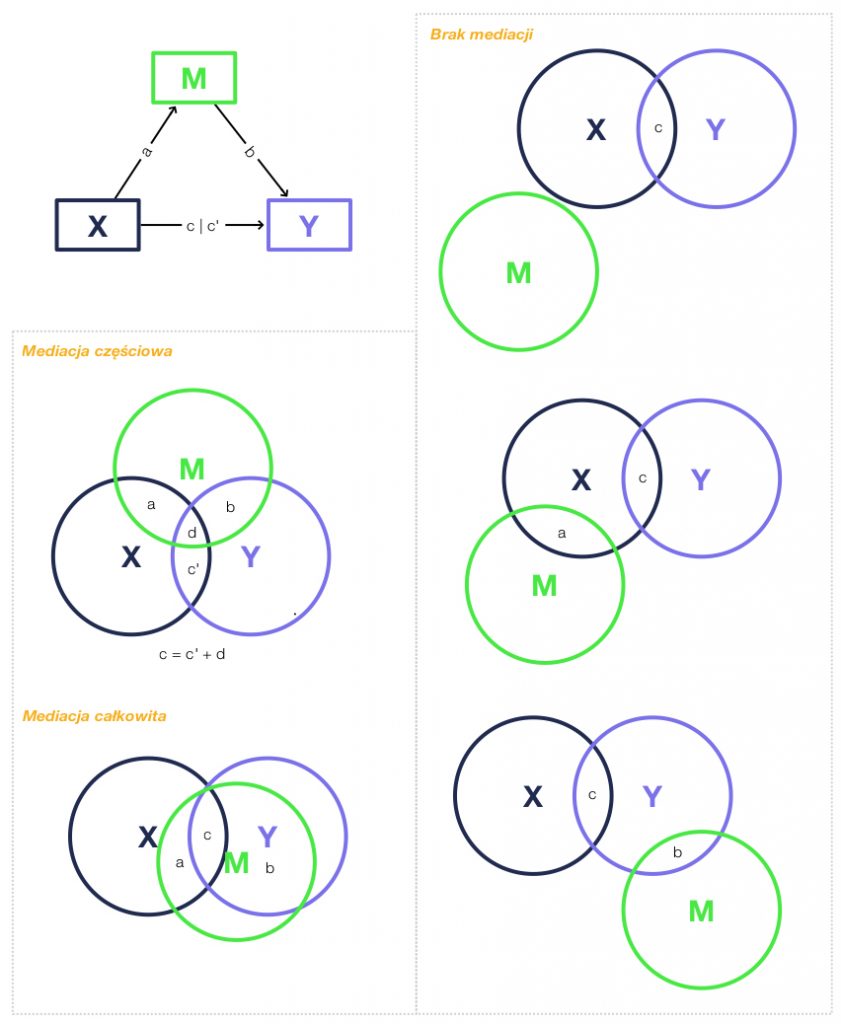
Zmienna M ma status mediatora, jeżeli spełniony jest warunek tzw. łącznej istotności (joint significance). W analizie wstępnej istotne okażą się związki obrazowane strzałkami a oraz b, co oznacza, że zmienna X wpływa na zmienną Y za pośrednictwem zmiennej M (strzałki a i b: zmienna X wpływa na M, zaś zmienna M wpływa na Y). Związek c, zmiennej X z Y zmienia się (istotnie słabnie lub pojawia się w przypadku supresji, stąd druga wartość: c’), jeżeli uwzględnić w analizie (kontrolować statystycznie) dwa pozostałe związki a i b.

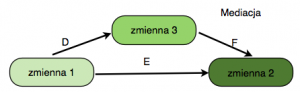
Mediacja opisywana tutaj to idealny przypadek, ale w realnych badaniach dużo częściej będziemy mieli do czynienia z mediacją częściową lub supresją (mediacją o przeciwnym działaniu: c < c’). Aby lepiej “zobaczyć” konieczność istnienia relacji na wstępie oraz różnice między mediacją częściową a całkowitą zamieszczam pieć diagramów kołowych przedstawiających wariancję poszczególnych zmiennych w modelu i ich możliwe wzajemne relacje.

W przypadku badań eksperymentalnych najbardziej adekwatnym sposobem testowania mediacji jest dokonanie dwóch analiz regresji² szacujących kolejno:

• wpływ zmiennej niezależnej (X) na pośredniczącą (M),
• wpływ zmiennej niezależnej (X) i pośredniczącej (M) na zmienną zależną (Y).

O tym, że zmienna (M) ma status mediatora można wnioskować, gdy uzyska się istotne współczynniki regresji dla relacji a i c, a druga analiza ujawni także istotny współczynnik regresji b. Równocześnie współczynnik regresji c’ powinien spaść do zera lub przynajmniej istotnie zmaleć w porównaniu z analogicznym współczynnikiem uzyskanym w analizie pierwszej.

Do oceny istotności efektu pośredniego najłatwiej skorzystać z testu Sobela (N > 50) lub Aroiana (N < 50) - jest to test pozwalający stwierdzić, czy dana zmienna faktycznie pełni rolę mediatora bazujacy na wielkości współczynników i ich błędów standardowych. W tym celu po przeprowadzeniu powyższych analiz regresji ich współczynniki wystarczy wpisać do kalkulatora na na tej stronie aby otrzymać odpowiedź.

Jeszcze łatwiejsze i bezpieczniejsze (w sensie unikania błędów) jest użycie pakietu mediation w środowisku R lub jakiegoś programu do równań strukturalnych SEM (np. pakietu lavaan, który poza R można także użyć w konsoli darmowego programu JAMOVI, do którego moduł MedMod też przeprowadza proste analizy mediacji). Zachęcam do wypróbowania tych pakietów, ponieważ efekty mediacyjne rzadko mają rozkłady normalne, a wspomniane programy oferują poza korektami bootstrapowymi na kształt rozkładu, także bardziej zaawansowane sposoby analizy, np. CMA - Causal Mediation Analysis.

Przykład takiej analizy w języku R dla prostego modelu powiązań między motywacją, aktywnością, napotykanymi barierami oraz wynikami w sporcie przedstawiam tutaj.

Przykładowy opis wyników analizy mediacji lub moderacji

Moderacja

A moderation test was run, with XXX as the predictor, YYY as the dependant, and MMM as a moderator. There was a significant main effect found between XXX and YYY, b =  1.23, 95% CI [1.11, 1.34], t = 21.38, p <.001, η_p² = .04 and nonsignificant main effect of MMM on YYY b =  1.05, 95% CI [0.72, 1.38], t = 1.28, p = .341, η_p² = .01. There was a significant interaction found by MMM on XXX and YYY, b =  0.05, 95% CI [0.01, 0.09], t = 2.16, p  = .031, η_p² = .04. It was found that participants who reported higher than average levels of MMM experienced a greater effect of XXX on mental distress (b =  1.35, 95% CI [1.19, 1.50], t = 17.1, p <.001, β = .24), when compared to average or lower than average levels of MMM (b =  1.23, 95% CI [1.11, 1.34], t = 21.3, p <.001, β = .14; b =  1.11, 95% CI [1.05, 1.27], t = 13.8, p <.001, β = .04, respectively). From these results, it can be concluded that the effect of XXX on YYY is moderated by MMM.

Mediacja

A mediation analysis was conducted to examine the mediating effect of MMM on XXX and YYY. The total effect of the model was found to be significant, b = 1.33, 95% CI [1.21, 1.45], z = 21.69, p < .001. It was found that there was a statistically significant direct effect, b = 1.28, 95% CI [1.15, 1.41], z = 19.66, p < .001. A statistically significant indirect effect was also found, b = 0.05, 95% CI [.002, .096], z = 2.05, p = .040. These results suggest that MMM partially (23%) mediated the relationship between XXX and YYY.

Footnotes

1. Założenia moderacji: 1) Zmienne zależne i niezależne powinny być mierzone na skali ciągłej. 2) Powinna istnieć zmienna moderująca, która jest zmienną nominalną z co najmniej dwiema grupami. 3) Zmienne będące przedmiotem zainteresowania (zmienna zależna oraz zmienne niezależne i moderujące) powinny mieć związek liniowy, który można sprawdzić za pomocą wykresu rozrzutu. 4) Dane nie mogą nie moga być wspołliniowe. 5) Nie powinno być znaczących wartości odstających, a rozkład zmiennych powinien być w przybliżeniu normalny.

2. Założenia mediacji: 1) Zmienne zależne, niezależne i pośredniczące muszą mieć skalę ciągłą. 2) Zmienne będące przedmiotem zainteresowania powinny mieć związek liniowy. 3) Dane nie mogą wykazywać współliniowości. 4) Nie powinno być niepożądanych wartości odstających, a rozkład zmiennych powinien być w przybliżeniu normalny.