Poradnik: jak wyznaczyć wielkość grupy badanej?

Zakładam, że wiedza o tym, czym jest błąd I-ego ¹ i II-go ² rodzaju jest znana. Wyznaczanie wielkości próby ma sens PRZED badaniem. Po przeprowadzeniu badania analiza mocy ma inny sens (poza wskazaniem dlaczego źle zaplanowaliśmy badanie) – w razie braku istotności dla odrzucenia hipotezy zerowej podpoiwada, czy brak efektu nie jest przypadkiem pokłosiem zbyt małej próby. Ale wróćmy do wyznaczania potrzebnej wielkości próby, jeśli stosujemy ideologię NHST³.

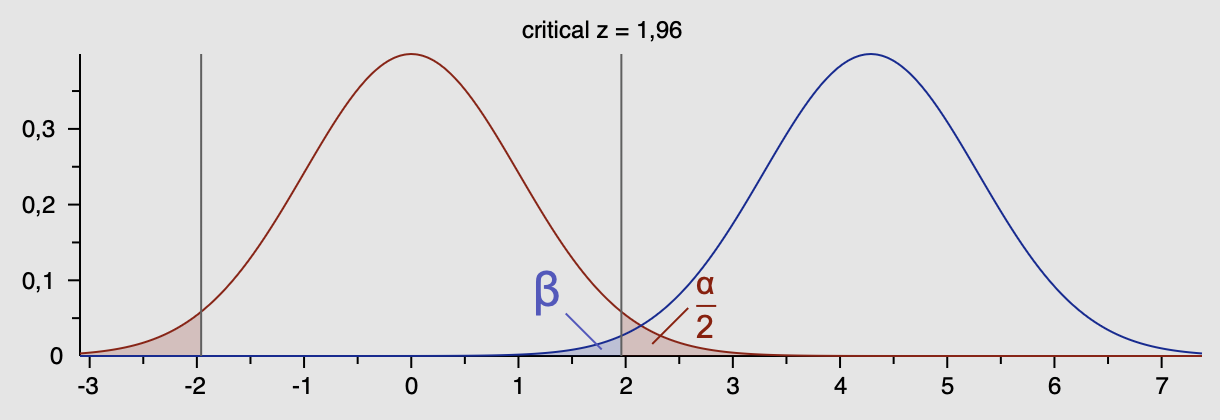
Dla planu badawczego, w którym porównać chcemy 2 grupy problem wyznaczenia ich przybliżonej wielkości przy założonej poziomach: błędu \(\alpha\) i mocy testu \(1-\beta\) może być rozwiązany w oparciu o równanie:

\(n_j \ge \frac{2 \cdot z\_{cv}^2}{d^2}\),

gdzie \(z_{cv}\) jest wartością krytyczną różnicy z rozkładu normalnego dla przyjętych założeń, a \(d\) jest wielkością efektu.

Dla przykładu, załóżmy, że średnia wartość interesującej nas zmiennej, w badaniach, które ktoś przeprowadził lub są jakoś podobne ⁴, w grupie kontrolnej wynosi \(\overline{Y}_c = 11.8\), grupa badawcza ma zmienną na poziomie \(\overline{Y}_b = 12.7\), a odchylenie standardowe w populacji ⁵ \(s = 1.5\).

Dla przyjętych danych efekt, czyli standaryzowana średnia różnica będzie wynosiła:

\(d = \frac{12.7 - 11.8}{1.5} = 0.6\).

Dla badania, w którym wystarczy nam 70% mocy (czyli \(1-\beta = 0.70\)), dla testu dwustronego i zakładanego błędu I-go rodzaju \(\alpha = 0.05\) oszacowana wielkość każdej grupy, to:

\(n_j \ge \frac{2 \cdot 2.485^2}{0.6^2} \ge \frac{2 \cdot 6.175225}{0.36} \ge 34.3 \approx 35\)

Jeśli zwiększymy moc, czyli chcemy mieć większą szansę na odrzucenie fałszywej hipotezy, do 80% i zmniejszymy poziom błedu I-go rodzaju, czyli zmniejszymy prawdopodobieństwo błędnego przyjęcia hipotezy o istnieniu efektu do 1% (\(\alpha = 0.01\)), to każda grupa będzie miała:

\(n_j \ge \frac{2 \cdot 3.418^2}{0.6^2} \ge \frac{2 \cdot 11.682724}{0.36} \ge 64.9 \approx 65\).

Patrząc na związki między wielkością efektu, błędem i mocą testu można też pomyśleć w drugą stronę. Jeśli planuję przebadać 100 osób (tj. po 50 w dwóch porównywanych grupach), to jaki efekt uda mi się zaobserwować, jeśli moc będzie na wymaganym poziomie 80% a poziom błędu pozostanie na 0.05? Otóż:

\(d \ge \frac{z_{cv}}{\sqrt{\frac{n_j}{2}}} \ge \frac{2.802}{\sqrt{\frac{50}{2}}} \ge \frac{2.802}{5} \ge 0.5604\).

Przy 100 próbie, porównując dwie grupy i przyjmując powyższe założenia możemy wykryć efekt o wielkości co najmniej 0.56. Większe efekty nie sprawiają problemu, mniejsze oznaczają spadek mocy badania i wejście w obszar, w którym nie wiemy, czy efektu nie ma, czy też nam się nie udało go stwierdzić.

---

Jeśli chcesz wyznaczyć wielkość próby, moc, efekt lub błąd dla innych planów badawczych (więcej grup, schematy korelacyjne, itp.) to ułatwieniem będzie użycie programu G*Power udostepnianego przez Uniwersytet Heinricha Heine w Dusseldorfie. Można też policzyć to wszystko dla prostych planów w Jamovi z modułem jpower lub w R z pakietem pwr.

---

Tabela 1. Wartości krytyczne różnicy rozkładu normalnego \(z\) przydatne dla wyznaczania wielkości prób dla często spotykanych założeń

Power	\(\alpha=.05\) jednostronny	dwustronny	\(\alpha=.01\) jednostronny	dwustronny
0.70	2.170	2.485	2.846	3.101
0.80	2.487	2.802	3.168	3.418
0.90	2.927	3.242	3.608	3.858
0.95	3.290	3.605	3.972	4.221

Wartości z premedytacją zaokrąglone są do góry. Postuluje się, aby moc w badaniach była rzędu 95% lub 99%.

Wersja PDF tej strony

Footnotes

1. Inaczej: błąd pierwszego typu, alfa-błąd, ang. false positive − błąd polegający na odrzuceniu hipotezy zerowej (o braku efektu), która w rzeczywistości nie jest fałszywa. Oszacowanie prawdopodobieństwa popełnienia błędu pierwszego rodzaju oznacza się symbolem \(\alpha\) (mała grecka litera alfa) i nazywa poziomem istotności testu.

2. Inaczej: błąd drugiego typu, błąd przyjęcia, beta-błąd, ang. false negative − błąd polegający na nieodrzuceniu hipotezy zerowej, która jest w rzeczywistości fałszywa. Oznaczany przez \(\beta\). \((1 - \beta)\) to moc testu.

3. Czyli Null Hypothesis Significance Testing.

4. Możemy też te wartości w realistyczny sposób założyć.

5. Jeśli ta wartość jest niedostępna możemy ją również próbować oszacować.